DB에서 데이터를 가져오는 방법에는 전체 데이터를 조사하는 Full Scan 방법과 인덱스 파일을 이용하는 Indexed Access 방법이 있다.
Full Scan 방법은 데이터 파일의 레코드를 순차적으로 확인하는 방법으로 매우 느리다.
Indexed Access 방법은 데이터파일과 구분되는 인덱스 파일에 접근해서 특정 레코드의 위치를 찾는 방법이다.
Indexed Access의 두 가지 종류
- Ordered indices : searc key가 정렬된 형태
- Hash indices : 해시 함수를 이용해 search key를 균등하게 버켓에 분포됨
ordered index

search key가 정렬된 상태. 인덱스 파일을 순차적으로 내려가면서 레코드를 찾음.
Full Scan 방법과 차이
- Data file의 크기 >>>> Index File의 크기
- 데이터 파일을 순차적으로 접근할 경우 매우 많은 Block들이 buffer를 거치게됨.
- 인덱스 파일을 순차적으로 접근할 경우 인덱스 파일이 훨씬 적은 Block으로 나눠져있기 때문에 훨씬 적은 Block이 buffer를 거침
- 아래의 경우 id=83821인 레코드를 찾을 때, 인덱스 파일을 사용하면 블록을 하나만 거치면 되지만, 인덱스 파일을 사용하지 않으면 6 개의 블록을 거쳐야함.

(Buffer와 Block은 앞의 글 참조 - Block을 적게 거칠수록 속도가 빠름)
Index access 의 단점 - Update
- 데이터 파일이 변경되면 인덱스파일도 변경해줘야함. - maintanance 비용
Primary index, Seconadary Index
Primary index (clustering index)
- (usually) primary key를 search key로 잡은 인덱스
- 딱 하나만 존재함 - DBMS가 자동으로 생성
- 인덱스 파일 순서와 데이터파일의 순서가 같음
Secondary index (non-clustering index)
- 데이터 파일과 순서가 다른 index
- 여러개 존재 가능 - 사용자가 직접 생성
Hashing
해싱을 이용한 file organization

해시함수를 이용해 버킷에 데이터를 분배한다.
DB에서 하나의 Block이 하나의 버킷 역할을 하게된다
버킷의 공간이 부족하면(overflow) 새로운 block을 사용함 - overflow chaining

Physics 레코드를 찾을 경우, 해시함수에 이를 넣고 나온 값으로 블록(버킷)에 접근.
해당 블록에서 순차로 내려가며 Physics 레코드를 찾는다.
Hash Index

file organization 뿐만 아니라 index-structure에도 해싱이 사용될 수 있다.
성능이 빠르지만, 데이터를 조회할 때 equal 연산만 가능하다. (범위 연산이 안됨) - DBMS에서 사용되지 않는 이유
B+ Tree Index Files
B+ Tree는 insert, delete overhead와 space overhead 라는 단점이 있지만, 장점이 더 크기 때문에 DBMS에서 인덱싱을 할 때 실제로 사용하는 방법임

B+ 트리 구성
- n-1 개의 search-key value K1, K2, ... , Kn-1
- n 개의 pointer P1, p2, ..., Pn
- 각 노드는 disk block임
B+ 트리의 조건 - 각 노드가 50% 이상 채워져있고, 루트-리프 길이가 같은 트리
- 모든 리프노드에서 루트까지의 높이가 같다
- 중간 노드는 n/2 개 ~ n 개의 자식을 갖는다
- 리프 노드는 (n-1)/2 개 ~ n-1 개의 vlaue를 갖는다


- K : search-key values
- P : search-key와 쌍으로 묶인 searc-key의 파일 레코드를 가리키는 포인터
- Pn : n 번째 P는 그다음 리프 노드를 가리킨다.
- search-key는 정렬된 상태임


- K : search-key values
- P : 자식 노드를 가리키는 포인터
- Pi 는 k(i-1)이상 k(i)미만인 search-key values를 갖는 자식 노드를 가리킴
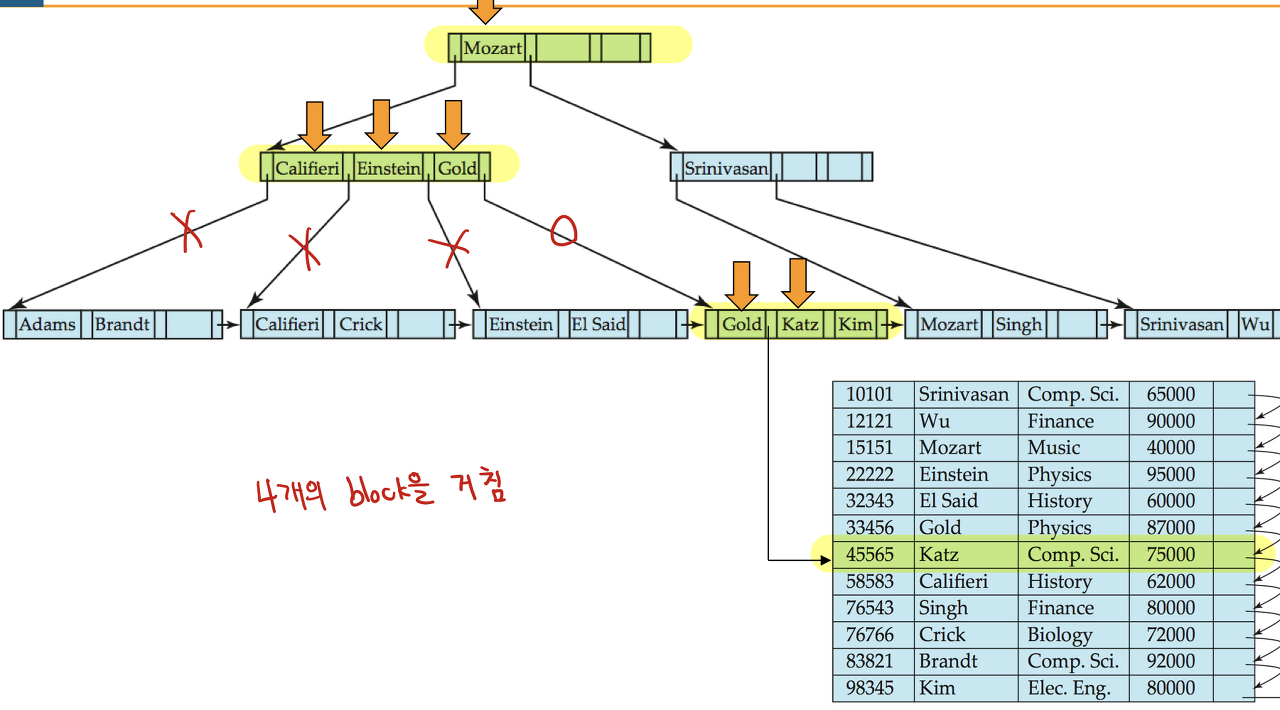
name = Katz 레코드 찾기 - 4개 블록 거침
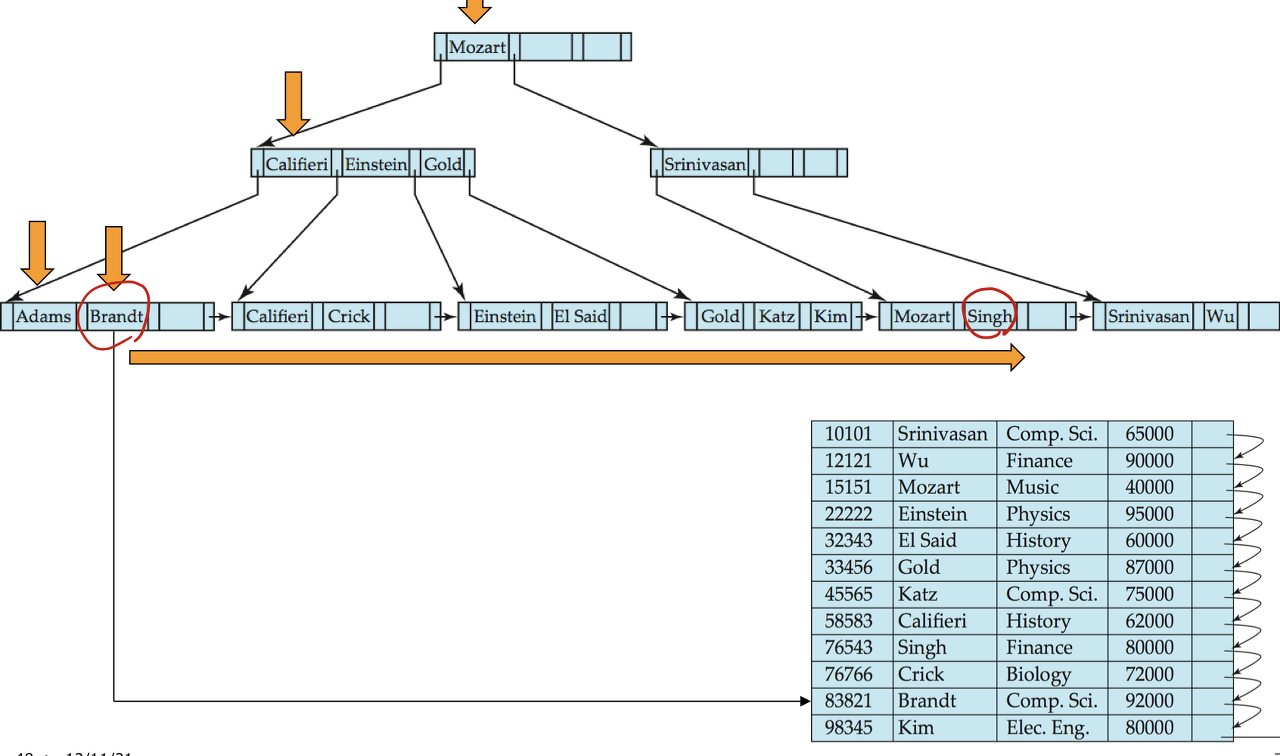
name ≥ Brandt and name ≤ Singh 레코드 찾기 - 4 개 블록 거침
범위 연산도 가능하다!
n 값의 결정


search-key size * (n-1) + pointer size * n ≤ 디스크 블록 크기
- 조건을 만족시키는 n 중에 가장 큰 정수 값을 n으로 결정한다.
- search-key size는 search key 타입의 크기 (테이블에서 결정)
- name char(12)를 search-key로 잡을 경우 크기는 1*12 = 12
B+ Tree의 높이
child가 최대 n 개에서 n/2 개이므로 log n (K) [올림] <= H <= log n/2 (K) [올림]
- n/2나 log한 결과 값 모두 올림 처리한다.
- K는 search-key vlaues의 갯수
B+ 트리와 Hashing
where a = b 같은 equal 연산의 경우 해싱이 B+Tree 보다 성능이 좋음
where a≤ b 같은 범위 연산의 경우 해싱은 불가능, B+Tree는 가능
reference : 상명대학교 김종욱 교수님
'컴퓨터과학 > 데이터베이스' 카테고리의 다른 글
| [데이터베이스] Storage and File Structure - Block, File organization, Fixed/Variable Records 저장 방식 (0) | 2021.12.19 |
|---|---|
| [데이터베이스] Entity-Relationship Model - 모델링, ERD, 관계형 스키마 (0) | 2021.12.14 |
| [데이터베이스] Data Analytics with SQL - DW, OLAP (0) | 2021.12.05 |
| [데이터베이스] SQL 총정리 1 (0) | 2021.10.27 |
| [MySQL] SQL 추가 문법 정리 - 프로그래머스 SQL 고득점 kit (0) | 2021.03.01 |



댓글